Lecture 10 - Ordered, Sorted, Binary Search, and Sets

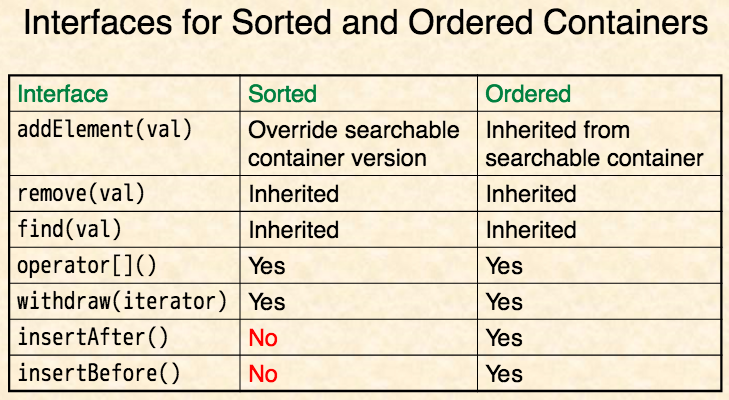
Linked List only preferred over an array when doing a lot of insertAfter(specific) and insertBefore(specific), or remove(iter)?

Binary Search in Sorted Container

int search(double a[], double val, int left, int right) {
    while(right >= left) {  // loop at most k times, k = log(n), O(log n)
        int mid = left + (right - left) / 2;
        if (val == a[mid]) return mid;   // found elt
        if (val < a[mid]) right = mid - 1;   // check < first
        else
            left = mid + 1;
    }  // n is split in half each loop
    return - 1;  // didn't find elt
}

Better Binary Search in Sorted Container

int search(double a[], double val, int left, int right) {
    int mid = left;
    while(right >= left) {
        mid = left + (right - left) / 2;
        if (val > a[mid]) left = mid + 1;  // check > first
        else
            right = mid - 1;    // if val < a[mid]
    }
    return mid;
}

STL Binary Search

BINARY SEARCH
binary_search() returns a bool

FIND LOCATIONS in terms of ITERATORS?
Other methods of BINARY SEARCH
lower_bound()
upper_bound()
equal_range()

Comparators (Functors)

• Given elts a and b, tell if a < b

Searchable Containers as Sets

STL Set Operations:

• Union OR
• Intersection AND
• Set-difference AND-NOT
• Symmetric Difference XOR (o-plus symbol or o-minus symbol)
  • Set of all objects that are in either A or B, but not both
• Cartesian Product (A x B)
  • Set whose members are all possible ordered pairs (a, b), where a is a member of A, b is a member of B
    • (1, 2), (1, 4), (2, 2) ,...
  • All possible pairs (two elts): A x B = size(A) x size(B)
• Power Set (P(A))
  • Set whose members are all possible subsets of A
  • 2^size(A) subsets
• isElement exists
• isEmpty
• addElement

Set_Union()

template<class InIterator1, class InIterator2, class OutIterator, class Pred>  // 4 classes
OutIterator set_union(InIterator1 first1, InIterator1 last1, InIterator2 first2,  // 4 input iterators
                      InIterator2 last2, OutIterator result, Pred pred) {         // 1 out Iter, 1 predicate
        while(first1 != last1 && first2 != last2) {
             if(pred(*first1, *first2))
                  *result++ = *first1++;   // set1 elt < set2 elt, so output set1's elt, increment set1
             else if (pred(*first2, *first1))
                  *result++ = *first2++;   // set2 elt < set1 elt, so output set2's elt, increment set2
             else {
                  *result++ = *first1++;   // set1 elt == set2 elt, so output an elt from either set1 or 2,
                                           //  (in this case we chose set1) and iterate both sets
                  ++first2;
             }
        }
        while (first1 != last1) *result++ = *first1++;  // remaining elts, if one set is larger than other
        while (first2 != last2) *result++ = *first2++;
        return result; // sorted union of 2 sets
}

Union-Find Data Structure

Idea 1: every disjoint set should have its unique representative (selected elt)

Idea 2: Compare representatives to tell if k and m are in the same set O(n) for updates

Idea 3: When performing union of 2 sets, update the smaller set

Idea 4: Don't store representative for each elt

Idea 5: Path compression, update the final representative for each elt in chain (later, in project 4)