3 Growth of Functions

Insertion sort is faster than merge sort at small inputs, but merge-sort is faster at large inputs

Asymptotic _efficiency - concerned with efficiency in the _limit

3.1 Asymptotic Notation

Don't abuse notation

Asymptotic notation, functions, and running times

Asymptotic usually used to describe running time (best, worst, average)

Ø-notation

Ø(g(n)) is set of functions, like f(n), that belong if there exist positive constants  c1 and c2 s.t. 
it can be "sandwiched" between the c1g(n) and c2g(n) graphs

Ø(g(n)) is a set, where function f(n) is member of the set
To indicate this, use
f(n) = Ø(g(n))

g(n) is an asymptotic tight bound for f(n)

Every function used with Ø notation is asymptotically non-negative

Ignore lower-order terms of asymptotically positive functions when doing tight bounds, and coefficients

Any quadratic function is Ø(n^2), can prove by dividing out n^2 and removing values with limit of 0 as n increases

Also can do proofs by contradiction

Any constant is a degree-zero polynomial with Ø(1) complexity

O-notation

O-notation gives us the asymptotic Upper Bound, or the worst-case complexity

Ø-notation implies O-notation and Ω-notation

Technically, we are abusing notation

Ω-notation

Ω-notation gives us Lower Bound, or the best-case complexity

No matter the input size, the running time will at least be a constant * g(n) for large n

Insertion sort is Ω(n), or best-case lower bound, and O(n^2), or worse-case upper bound

However, we can still say

In the Worse-case: Ω(n^2)

In the Best-case: O(n)

Anonymous functions are a way to represent lower-order parts

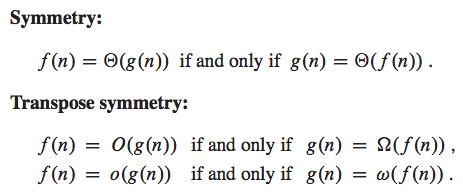
Trichotomy does not hold for asymptotic notatoin

Ex. sin(n) and cos(n) have no required <, =, or > due to oscillation

3.2 Standard Notations and Common Functions

Monotonicity

Monotonically increasing: $$f(m) \leq f(n)$$

Monotonically decreasing: $$f(m) \geq f(n)$$

Strictly increasing: f(m) < f(n), n is bigger than m

Strictly decreasing: f(m) > f(n)

Floors and Ceilings

Floor of x: Greatest integer $$\leq$$ x, represent by floor(x)

Monotonically increasing

Ceiling of x: Least integer $$\geq$$ x, represent by ceil(x)

Monotonically increasing

Modular Arithmetic

a _mod _n is the remainder of the quotient $$a / n$$

a is equivalent to b, modulo n

Polynomials

Polynomially bounded if f(n) = O(n^k)

Exponentials

Any exponential function with a base strictly greater than 1 grows faster than any polynomial function

Logarithms

Logarithms used here will be base 2, since many algorithms require splitting a problem into 2 parts

Poly-logarithmically bounded if f(n) = O(log^_{k} n)

Polynomials grow faster than any poly-logarithmic functions

Factorials

Stirling's Approximation gives us a weak bound

Functional Iteration

Iterated Log

Fibonacci Numbers

Golden Ratio

Grow Exponentially

3 - Complexity Analysis