Ch. 6 - Heapsort ( & Heaps)

6.1

Heapsort sorts in place, like insertion sort.

If memory is an issue, this is preferable to merge sort, since Heapsort stores O(1) array elts outside the input array at any time, like insertion sort?

Heapsort runs in O(n log n) time, like merge sort.

Heapsort uses a heap to manage information. The heap makes an efficient PQ, better than an array or hash table implementation since we need constant time access to extreme elements.

Heap Algorithms:

Max-Heapify: fix a subtree and make it max-heap

Build-Max-Heap: make a max heap from an unordered array

Heapsort: sort an array in place

max-Heap-Insert, heap-Extract-Max, heap-Increase-Key, heap-Maximum (see 6.5 PQs)

Heaps

Terminology:

Heap -> data structure

Heapsort -> sorting algorithm

Priority Queue -> abstract data type

Heap are good for extreme element access

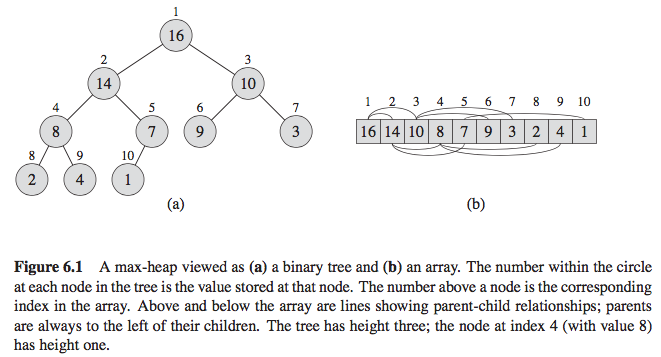
(Complete Binary) Heap DS: array object, nearly complete binary tree

Terminology for Binary Trees:

Complete: All levels are filled and leftmost

Nearly Complete: All levels except maybe last are filled and leftmost

Full/ Strict/ Proper: No nodes with only 1 child (never half-full)

Perfect: Complete and Full (like a triangle)

An array representation of a heap:

A.length: number of elts in array
A.heap-size: number of elts in heap stored in array

Root of tree is (1-indexed) A[1]

Code for Heap as Array

// 0-INDEXED
PARENT(i)
return (i - 1)  / 2

LEFT(i)
return 2i + 1

RIGHT(i)
return 2i + 2

HEIGHT(n)
return ceil(log(n + 1))

#1-INDEXED, NEED TO DO 0-INDEXING ON EXAMS
PARENT(i)
return floor(i / 2)

LEFT(i)
return 2i

RIGHT
return 2i + 1

Max-Heap Property: each node is (larger) than its children

Min-Heap Property: each node is (smaller) than its children

6.2 - Max_Heapify O(log n) or O(h)

maxHeapify(i):
    l = left(i) # these are array pointers?
    r = right(i)
    if l < A.size and A[l] > A[i]:
        largest = l
    else:
        largest = i
    if r < A.size and A[r] > A[largest]:
        largest = r
    if largest ≠ i
        swap A[i] and A[largest]
        maxHeapify(largest)

Recurse until the subtree at (including) i satisfies max-heap property

Confusion: the recursive call to index largest is really the original value i, only i is now lower in the subtree. Largest at the recursive call is not actually the largest element in the subtree?

6.3 - Build_Max_Heap/ Fix-Up O(n) ~tricky

Building bottom up, but skipping the leaf nodes (may be on multiple levels)

Just go through all nodes above leaves and run Max_Heapify
Converts array to max-heap

buildMaxHeap():
    for i = (A.size - 2) / 2..>= 0:
        maxHeapify(i)

Fix-Down (Top-Down) might actually be better, but since this avoids the leaf nodes they're more comparable

6.4 - Heapsort O(n lg n)

Keep dequeue-ing the highest-priority element from a PQ, in-place sort with array implementation

First call buildHeap, then run for loop that calls maxHeapify n-1 times

void heapsort(Item heap[], int n) {
    buildHeap(heap, n);
    for (int i = n - 1; i >= 1; --i) {
        swap(heap[i], heap[0]);
        fixDown(heap, i - 1, 0);
    }
}

Other Useful Functions:

Increase Key Priority (Fix-Up)

This can be called after adding a new key to the end of a heap array, or after increasing the value of a key already in the heap.

These functions are usually used when working with a PQ, since now values can be changed

// The 'i' in parent(i) is represented as k /= 2, so heap[k /= 2] is essentially the parent node

// Insert function: first line
void insert(Item newItem) {
    ++heapsize;
    heap[heapsize] = newItem;
    fixUp(heap, heapsize);
    // while(k > 1 && heap[k / 2] < heap[k]) {
    //     swap(heap[k], heap[k / 2]);
    //     k /= 2;  // this is the parent 'node'
}

// fixUp function
void fixUp(vector heap[], int k) {
    while(k > 1 && heap[k / 2] < heap[k]) {
        // keep looping until root or until max-PQ condition is met
        swap(heap[k], heap[k / 2]);
            // swap child with parent
        k /= 2; 
            // this is the parent 'node'
    }
}

# using parent(i)
increaseKey(i, k):
    if k < A[i]:
        error "new key is smaller than current key"
    A[i] = k
    increaseKey(size - 1, k)  #implementation in below 3 lines
    # while i ≥ 0 and A[parent(i)] < A[i]:
    #     swap A[i] and A[parent(i)]
    #     i = parent(i)

6 - Heapsort and PQs